Prerequisite

You should have a pipeline of analysis for ERPs/ERFs.

Goal of this tutorial

This tutorial explains how to perform ERP/ERF analyses based on surrogate stimuli.

It takes the example of heartbeat-evoked responses (ERPs/ERFs elicited by heartbeats), but can be applied to any other sort of ERP/ERF.

Step-by-step guide

1. Rationale

Heartbeat-evoked responses are ERPs/ERFs elicited by (or locked to) heartbeats (Schandry et al 1986). One question that often arises is whether what we are measuring is a true response to a heartbeat stimulus or a sampling of ongoing slow fluctuations.

In the example below, the red stimulus is the stimulus of interest, say heartbeats. When you sample the data locked to the red stimulus, you obtain a difference in brain activity between condition 1 and condition 2. However, this difference is carried by differential baseline levels of brain activity (in blue). This means that if you lock ERPs to random timings, say the yellow 'surrogate' heartbeats on the right, you also obtain the same difference between conditions 1 and 2.

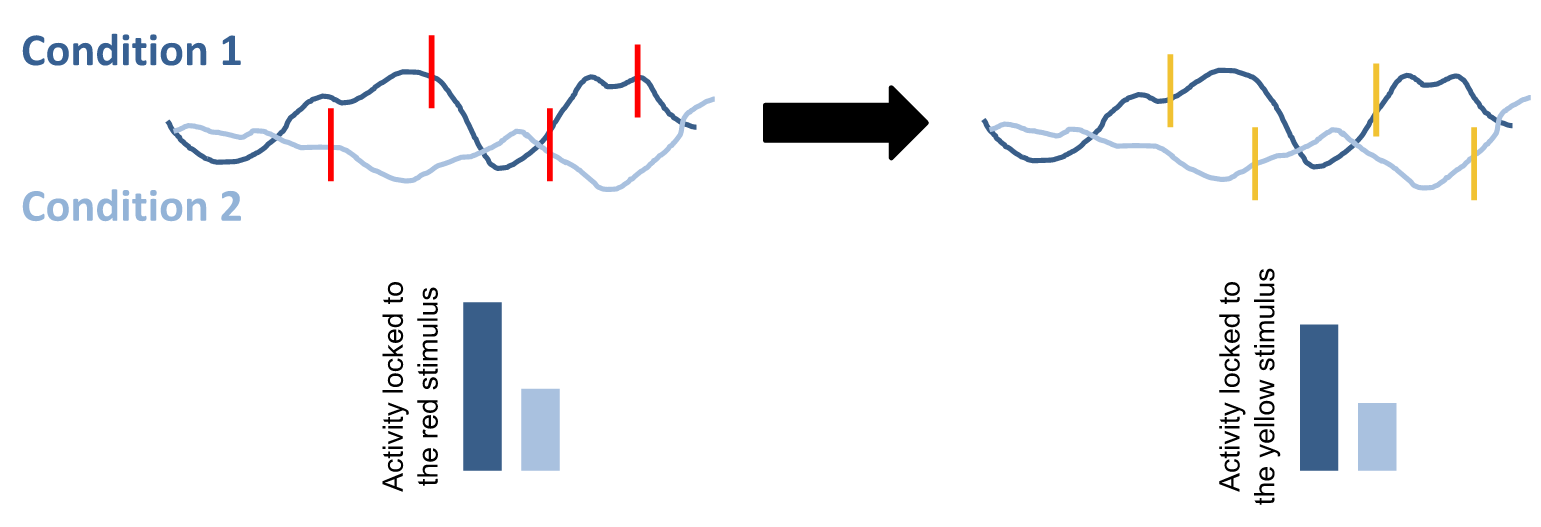
On the contrary, if you obtain a difference between condition 1 and condition 2 with the red stimulus, but you do not obtain a difference when you lock ERPs to surrogate heartbeats, you can rule out the hypothesis that your ERPs were due to different levels of brain activity. This suggests that heartbeats were truly originating a brain response.

This is the rationale for the surrogate analysis: taking random (or quasi-random) timings on the data of interest, perform the analysis locked to these timings and test whether the results still hold. We repeat this procedure a large number of times.

Keep in mind that for this procedure to be valid, the surrogate timings have to follow all constraints applied to the original timings. For example, heartbeats have a certain interbeat interval distribution, so surrogate heartbeats have to comply with this distribution as well.

(See Park et al 2014, Babo-Rebelo et al 2016 for examples)

2. Implementation

To implement this analysis you need to perform the following steps:

have a clear and clean analysis pipeline of your original results
extract the timings of your stimuli (heartbeats for example)
shuffle these timings across trials (with the function 'randperm', in Matlab, for example). This means that heartbeats of trial i are attributed to trial j, and heartbeats of trial j are attributed to trial k...
run the analysis pipeline on these surrogate timings
extract a meaningful statistical effect size
perform steps 3, 4 and 5 a large number of times (100 or 1000 times for example)

By shuffling the original timings across trials (instead of generating new timings), you keep the original constraints of the data.

Remember that "random" numbers are generated in Matlab using a deterministic algorithm, which means that you will get the same values each time you restart Matlab. If you want to run subsets of randomizations in different Matlab sessions, you have to reinitialize the random number generator, otherwise all your Matlab sessions will give the same results. See here for how to implement this.

3. Results

For each randomization, you have to extract a meaningful statistical effect size. If your original analysis was based on a cluster-based permutation test, you can extract at each permutation the maximal (or minimal) sum of t-values obtained. After the 100 or 1000 permutations, you will count the proportion of permutations leading to a larger effect than the original one. This corresponds to computing a Monte-Carlo p-value.

Of course you expect that none of the permutations (or a very small number of them) lead to a statistical result that was equal or larger than the original one you obtained.

CENIR

Creating surrogate data: swapping cardiac beats across trials